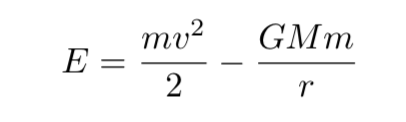What follows are the opening paragraphs of a pdf document giving an argument for controlled natural languages in mathematics.
At the recent Big Proof 2 conference in Edinburgh, I realized that a case must be made for developing a controlled natural language for mathematics. There is little consensus on this issue, and mathematicians and computer scientists tend to line up on opposite sides. Some are outright dismissive of the idea. Little research is happening. While making the case below (giving the mathematician’s side), I’ll also review and respond to some of the computer scientists’ objections.
Controlled Natural Languages (CNL)
By controlled natural language for mathematics (CNL), we mean an artificial language for the communication of mathematics that is (1) designed in a deliberate and explicit way with precise computer-readable syntax and semantics, (2) based on a single natural language (such as Chinese, Spanish, or English), and (3) broadly understood at least in an intuitive way by mathematically literate speakers of the natural language.
The definition of controlled natural language is intended to exclude invented languages such as Esperanto and Logjam that are not based on a single natural language. Programming languages are meant to be excluded, but a case might be made for TeX as the first broadly adopted controlled natural language for mathematics.
Perhaps it is best to start with an example. Here is a beautifully crafted CNL text created by Peter Koepke and Steffen Frerix. It reproduces a theorem and proof in Rudin’s Principles of mathematical analysis almost word for word. Their automated proof system is able to read and verify the proof.
Theorem [text in Naproche-SAD system] If 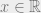 and
and 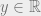 and
and 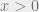 then there is a positive integer
then there is a positive integer  such that
such that 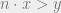 .
.
Proof Define  . Assume the contrary. Then
. Assume the contrary. Then 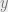 is an upper bound of
is an upper bound of  . Take a least upper bound
. Take a least upper bound  of
of  .
. 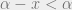 and
and  is not an upper bound of
is not an upper bound of  . Take an element
. Take an element  of
of  such that not
such that not 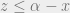 . Take a positive integer
. Take a positive integer  such that
such that 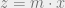 . Then
. Then  (by 15b).
(by 15b).

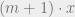 is an element of
is an element of  . Contradiction. Indeed
. Contradiction. Indeed  is an upper bound of
is an upper bound of  . QED.
. QED.
In my view, this technology is undervalued. I feel like a stock advisor giving tips here, but I see it as an opportune time to invest heavily in CNLs.
The argument
Here is an outline of the argument that I will develop in the paragraphs that follow.
- Technology is still far from being able to make a semantic reading of mathematics as it is currently written.
- Machine learning techniques (in particular, deep neural networks) are still far from a semantic reading of mathematics.
- Linguistic approaches are still far from a semantic reading of mathematics as it is currently written.
- Mathematicians are still far from the mass adoption of proof assistants.
- Adoption has been gradual.
- Structural reasons hinder the adoption of proof assistants.
- There is value in bridging the gap between (1) and (2).
- CNL technology works now and can help to bridge the gap.
1. Technology is still far from making a semantic reading of mathematics as it is currently written
In my view, the current champion is WolframAlpha, in its ability to answer natural language queries about mathematics.
1a. Machine learning (neural networks) are still far from a semantic reading of mathematics
Recent advances in machine learning, such as AlphaZero, have been spectacular. However, some experts point to major unsolved technological problems.
I visited Christian Szegedy’s group at Google in Mountain View and April and attended their talks at AITP in Austria the same month. They have ambitions to solve math (to use their mind-boggling phrase) in the coming years. Their ambitions are inspiring, the resources and research methodologies at Google are grandiose, but I would not personally bet on their time frame.
Their current focus is to use deep neural networks to predict a sequence of tactics that will successfully lead to new formal proofs of lemmas. These are all lemmas that have been previously formalized by John Harrison in his HOL Light libraries on real and complex analysis. As things stand now, other long-established technologies (such as hammers) have had similar success rates in formal proof rediscovery. Thus far, Google is not ahead of the game, but they are progressing quickly.
David Saxton (at DeepMind) spoke at the Big Proof 2 conference in May. He described a new large machine-learning dataset of school-level problems in areas such as arithmetic, algebra, and differential calculus. Currently the machine learning success rates are poor for many of these categories. The dataset is meant to stimulate machine learning research on these topics.
Deep neural networks have not been successful thus far in learning simple algorithms. In particular, deep neural networks cannot currently predict with much accuracy the answer to elementary sums of natural numbers. What is 437+156? Can a machine learn the algorithm to add? School-level math problems require more than parsing mathematical text. Nevertheless, parsing of mathematical text remains an unsolved challenge. They write in the introduction to their recent paper:
One area where human intelligence still differs and excels compared to neural models is discrete compositional reasoning about objects and entities that ‘algebraically generalize’ (Marcus, 2003). Our ability to generalise within this domain is complex, multi-faceted, and patently different from the sorts of generalisations that permit us to, for example, translate new sentence of French into English.
Here is an example of a challenging problem for machine learning from their paper. What is 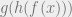 , where
, where  ,
, 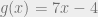 , and
, and 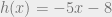 ?
?
Based on their paper, it seems to me that semantic parsing of research level mathematics is still years away.
1b. Linguistic approaches are still far from a semantic reading of mathematics as it is currently written.
The most widely cited work here is Mohan Ganesalingam’s thesis “The
language of mathematics.” The thesis uses Discourse Representation
Theory from linguistics to analyze mathematical language.
Ganesalingam analyzes the language of mathematics as it is written in
real mathematical publications, in all of its organic complexity.
There is far too little research in this area. Here is his assessment.
Mathematics differs sufficiently from human languages that little linguistic theory can be used directly; most of the material must be rebuilt and reconstructed. But linguistics, at the very least, gives us general ideas about how we can formally analyse language: it gives us a mindset and a starting place. Thus, in very broad terms, our work may be regarded as `the application of linguistics to mathematical language’. This is almost untrodden ground; the only linguist to analyse mathematics, Aarne Ranta, notes that “Amazingly little use has been made of [mathematical language] in linguistics; even the material presented below is just an application of results obtained within the standard linguistic fragment […].” Ranta (1994)
Ganesalingam – Principia conference
Furthermore,
We demonstrate that no linguistic techniques can remove the ambiguity in mathematics. We instead borrow from mathematical logic and computer science a notion called the `type’ of an object… and show that this carries enough information to resolve ambiguity. However, we show that if we penetrate deeply enough into mathematical usage, we hit a startling and unprecedented problem. In the language of mathematics, what an object is and how it behaves can sometimes differ: numbers sometimes behave as if they were not numbers, and objects that are provably not numbers sometimes behave like numbers.
Ganesalingam – Principia conference
As I understand, Mohan’s work was mostly theoretical and although there were once plans to do so, it has not been implemented in any available software.
2. Mathematicians are still far from the mass adoption of proof assistants
2a. Adoption has been gradual
I have watched first-hand the gradual adoption of proof assistants by
mathematicians.
In 2001 when I first took up formalization, I knew only a few mathematicians who were even aware of proof assistants (Dan Bernstein, Carlos Simpson, Doran Zeilberger, …). That was the year I moved to Pittsburgh, and CMU already had a long tradition of formal proof in among logicians and computer scientists (Dana Scott, Peter Andrews, Frank Pfenning, Bob Harper, Jeremy Avigad, and so forth).
In 2008, Bill Casselman and I were guest editors of a special issue of the Notices of the AMS on formal proof that helped to raise awareness among mathematicians. This included a cover article by Georges Gonthier on the formal proof of the four color theorem. (All the authors of this special issue were together again at the BigProof2 conference.)
Homotopy type theory (HoTT) became widely known throug a special program at the Institute for Advanced study in 2012-2013, organized by V. Voevodsky, T. Coquand, and S. Awodey. A popular book on HoTT resulted from that program. Other programs followed, such as the IHP program on the semantics of proof and certified programs in 2014.
Major publishers in mathematics now publish on formal proofs. There have been notable success stories (formalizations of the Feit-Thompson theorem and the Kepler conjecture). Equally, there have been major industrial success stories (the CompCert verified compiler and the SeL4 microkernel verification).
In the last few years, several more mathematicians (or perhaps dozens if we include students) have become involved with Lean (but not hundreds or thousands).
Formal proofs are now regular topics online in places such as reddit and mathoverflow.
In summary, the landscape has changed considerably in the last twenty years, but it is still nowhere near mass adoption.
2b. Structural reasons hinder the adoption of proof assistants
There are reasons for lack of mass adoption. The reason is not (as some computer scientists might pretend) that mathematicians are too old or too computer-phobic to program.
If mathematicians are not widely adopting formalization, it is because they have already sized up what formalization can do, and they realizethat no matter its long term potential, it has no immediate use to them. Homotopy type theory and related theories are closely watched by mathematicians even if not widely used.
I realize that I am an exception in this regard, because I had a specific real-world situation that was solved through formalization: the referees were not completely able to certify the correctness of the Kepler conjecture and eventually they reached a point of exhaustion. It fell back on my shoulders to find an alternative way to certify a proof the Kepler conjecture.
Wiedijk has pinpointed the most important reason that proof assistants have not caught on among mathematicians: in a proof assistant, the obvious ceases to be obvious.
Kevin Buzzard has spoken about his frustrations in trying to get Lean to accept basic facts that are obvious to every mathematician. Why is 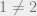 ? He has faced further frustrations in dealing with mathematically irrelevant distinctions made by proof assistants. For example, different constructions of a localization of a ring can lead to canonically isomorphic (but unequal) objects, and it is no small matter to get the proof assistant to treat them as the same object.
? He has faced further frustrations in dealing with mathematically irrelevant distinctions made by proof assistants. For example, different constructions of a localization of a ring can lead to canonically isomorphic (but unequal) objects, and it is no small matter to get the proof assistant to treat them as the same object.
3. There is value in bridging the gap between (1) and (2).
I’ll quote a few mathematicians (from Ursula Martin’s BigProof2 conference slides from the Breakthrough Prize interviews, 2014)
“I would like to see a computer proof verification system with an improved user interface, something that doesn’t require 100 times as much time as to write down the proof. Can we expect, say in 25 years, widespread adoption of computer verified proofs?” -J. Lurie
“I hope [we will eventually be able to verify every new paper by machine.]. Perhaps at some point we will write our papers… directly in some formal mathematics system.” – T. Tao
Timothy Gowers was part of a panel discussion at BigProof1 conference in 2017. He went through a list of automation tools that he would find useful and another list of tools that he would not find useful at all. One dream was to develop an automated assistant that would function at the level of a helpful graduate student. The senior mathematician would suggest the main lines of the proof, and the automated grad student would fill in the details. He also suggested improved search for what is in the literature, when you do not know the name of the theorem you are searching for, or even whether it exists. For this, full formalization is not needed.
Michael Kohlhase and others in his group have advocated “flexiformal” mathematics, as an interpolation between informal and formalized mathematics. They are also developing technology to translate between different proof assistants (or formal languages).
The Logipedia project also implements general methods to translate mathematics between formal languages, using a Logical Framework (Dedukti) and Reverse Mathematics.
An intended application of a large corpus of mathematics in a CNL would be big data sets for machine learning projects. Currently there is far too little data that aligns natural language mathematics with formal mathematics.
My dream is to someday have an automated referee for mathematical papers.
4. CNL technology works and can help to bridge the gap.
I believe strongly in the eventual mechanization of large parts of mathematics. According to a divide and conquer strategy for accomplishing this, we want to strike at the midpoint between current human practice and computer proof. In my view, CNLs do that. A million pages of this style of CNL is achievable.
4a. CNL has a long history
A brief history of the CNL Forthel (an acronym of FORmal THEoryLanguage) is sketched in K. Vershinin’s note. Koepke told me that Forthel (that is, fortel’, or фортель) means trick in Russian and that this is an intended part of the acronym.
Research started with V. Glushkov in the 1960s. A system of deduction was part of the system from the beginning (even if my interest is primarily in the language). A description of the language first appeared in the Russian paper “On a language for description of formal theories” Teoretischeskaya kibernetika, N3, 1970.
Research continued with V. Bodnarchuk, K. Vershinin and his group through the late 1970s. Most of the early development was based in Kiev.
The language was required to have a formal syntax and semantics. To allow for new definitions, “the thesaurus of the language should be separated from the grammar to be enrichable. On the other hand the language should be close to the natural language of mathematical publications.”
The development of the Forthel language development seems to have been intermittant. Andri Paskevich’s thesis in Paris gives a description of the language and deduction system as of the end of 2007.
Afterwards, development (renamed as Naproche-SAD) shifted to Bonn with Peter Koepke and his master’s student Steffan Frerix. The current Haskell code is available on github. In this document, I will use Forthel and Naproche-SAD as synonyms, although Forthel is the name of the controlled natural language, whereas Naproche-SAD includes a reasoning module connected to the E theorem prover.
In May 2019, Makarius Wenzel implemented a mode of Isabelle/PIDE for Naproche-SAD. It can be downloaded. This is currently the best way to interact with Naproche-SAD.
4b. The Forthel language has an elegant design
The text we produce is intentionally verbose and redundant. The aim is to produce texts that can be read by mathematicians without any specialized training in the formalization of mathematics. We want mathematicians (say after reading a one page description of our conventions) to be able to read the texts.
The ability to understand a CNL is an entirely different matter than to write or speak a CNL. The CNL might have invisible strict grammatical rules that must be adhered to. As Stephen Watt put it, there is a difference between watching a movie and directing a movie.
Our main references are Paskevich’s paper on Forthel (The syntax and semantics of the ForTheL language, 2007), his thesis at Paris XII and the Naproche-SAD source code.
Naproche-SAD achieves readability through a collection of tricks. The linguistics behind Naproche-SAD is actually quite elementary, and it is remarkable how English friendly it is with so little linguistics. One trick is the generous use of stock phrases (or canned phrases) that the user can supply.
Another trick is the use of free variants (synonyms), such as making set and the plural sets fully interchangeable synonyms. There are no grammatical notions of gender, case, declension, conjugation, agreement, etc. in Forthel. The needed forms are introduced as variants and the system does not care which are used.
Another trick is the use of filler words. These are words that are ignored by Forthel. For example, in many contexts indefinite and definite articles a, an, the are disregarded. They are there only for human readability.
The Naproche-SAD parser is written in Haskell. It is basically a simplified knock-off of the Haskell parsec parser library.
The grammar is not context-free (CFG). Some parser generators (such as LR(k) parsers) are not appropriate for our project.
Although the grammar is extensible, we can still describe the language by a finite list of production rules in BNF format. The collection of nonterminals cannot be changed. However, some of the nonterminals are designated as primitive. Primitive nonterminals differ from ordinary nonterminals in that new replacement rules can be added (by the user) to a primitive nonterminal. In this way, as mathematical text progresses, the grammar can be enriched with new constructions and vocabulary.
4c. Forthel language design principles
provide a template for future CNLs
This is work in progress. The point is that Forthel design is sufficiently generic that the language can be readily adapted to support back-end semantics of Lean’s dialect of CiC.
For this project, we recommend using the Haskell parsec parser library. Parsec is written as a library of parser combinators, with lazy evaluation, in a continuation style, with state stored in a parser monad.
If Lean4 has sufficiently powerful parsing capabilities, we can eventually port the project into Lean4. By using Haskell for our initial implementation, we make porting easier.
Actually, we combine two different parsing technologies: parsec style combinators and a top-down-operator precedence parser. The top-down-operator precedence parser is used for purely symbolic formulas. We describe below the rule used to extract sequences of symbolic lexemes that are shipped to the top-down-operator precedence parser. By including a top-down-operator precedence parser, we are able to add new symbolic notations with fine-grained levels of precedence.
We expect the grammar to be ambiguous. The parser should be capable of reporting ambiguous user input.
It seems to me that the biggest difficulty in writing a CNL for Lean will be the “last mile” semantics of Lean. By this, I mean the automatic inserting the correct coercions and casts along equality to produce a pre-expression that can be successfully elaborated and type checked by Lean. (I expect that automatically generated pre-expressions will frequently be off by casts along equality.)
Objections and counterarguments
At the BigProofs2 conference, several researchers made the argument that controlled natural languages are a step backwards from precise programming languages.
We should not abandon centuries of mathematical notational improvements
A sneering comparison was made between CNLs and the medieval practice of writing formulas and calculations out long-form in natural language. Significant progress in mathematics can be attributed to improved symbolic representations for formulas and calculations. It would be terrible to be forced in our language to write 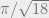 as pi divided by the square root of eighteen.
as pi divided by the square root of eighteen.
I agree. In fact, our controlled natural language is designed as a superset of Lean syntax. Lean is both a language of mathematics and a pure functional programming language similar to Haskell. Our augmented syntax loses none of that. We continue to write 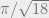 as such.
as such.
Nobody advocates abandoning notations that mathematicians find useful. A fully developed CNL includes all the great notational inventions of history such as decimal, floating point and other number formats, polynomial notation, arithmetic operations, set notation, matrix and vector notation, equations, logical symbolism, calculus, etc.
A CNL is also more than that, by providing precise semantics for mathematics in natural language.
Knuth, who has thought long and hard about mathematical notation, instructs that it is especially important “not to use the symbols 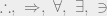 ; replace them by the corresponding words. (Except in works on logic, of course.)” The symbols are less fluent than the corresponding words. Knuth gives this example of a bad writing style:
; replace them by the corresponding words. (Except in works on logic, of course.)” The symbols are less fluent than the corresponding words. Knuth gives this example of a bad writing style:
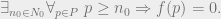
Another bad example from Knuth appears below in the section on examples.
We should not return to COBOL
Continuing with the criticism of CNL, some argue that CNLs are an unpleasant step in the direction of COBOL. Among the BigProof2 conference crowd, COBOL evokes Dijkstra’s assessment “The use of COBOL cripples the mind; its teaching should, therefore, be regarded as a criminal offence.” Still today, there is a strong distaste among some theoretical computer scientists (and principled programming language designers) of designs based on natural language.
Like COBOL, a CNL is self-documenting, English-oriented, and more verbose than ordinary programming languages. However, the features of COBOL that incite wrath have nothing to do with CNLs: the GOTO statement, lack of modularity, no function calls, no type checking on subroutine calls, no libraries, and so forth.
Lean is already readable
Some say that Lean is already readable and that a CNL is therefore wasted effort.
I find the level of readability of Lean to be similar to that of Coq. It is somewhat less readable than scripts in Mizar and Isabelle/HOL/Isar.
For those trained in Lean, the statements of definitions and theorems are readable, but most users find it necessary to jump incessantly from file to file within an environment such as VSCode (or emacs) because relevant context is spread through many files.
Generally, even those who write the scripts in Lean find it necessary to jump around in this manner to make sense of their own scripts. It is wonderful to have tools that allow us to jump around, but when that becomes the only possible mode of interaction, our thinking about mathematics becomes fragmented. (I may be old-fashioned in this worry of fragmentation.)
Proofs in almost all proof assistants are unreadable (in any sort of linear text-oriented fashion). Lean is no exception.
My impression is that few mathematicians would be willing to invest the necessary effort to read Lean scripts.
Here are some samples of Lean code. I do not mean to single out the authors of these files for criticism. The files are meant to be representative of Lean.
In a CNL, there is no semantic penalty for writing the fundamental theorem of algebra as follows.
Assume that 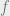 is a polynomial over
is a polynomial over 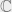 of positive degree. Then there exists a complex number
of positive degree. Then there exists a complex number  that is a root of
that is a root of 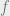 .
.
Documentation should be generated from source code, not vice versa.
Another argument is that we should generate natural language documentation from the formal text rather than the other way around. There are many successful examples of this approach, such as Mizar to LaTeX translation. These are useful tools, and I have no criticism of this.
The direction of code generation depends on the purpose. The source format is generally speaking the cleanest representation. A human will be directly involved in writing the source format. If the primary purpose is formalization, then formal scripts should be the source format from which others are generated. (Subtle differences in representation of mathematical concepts code can make a big difference in how painful the formal proofs are.) If the primary purpose is mathematical communication, then human-oriented language should be the source format. (Humans can be easily annoyed by the stilted language generated from formal representations.) Who should we ask for tolerance, the human or the computer?
Other variations appear in practice. In some projects there are two source formats and semantics-preserving translation from one to the other. For example, computer software can have a specification from which executable code might be automatically extracted, but for reasons of efficient execution it might be better to run an optimized hand-crafted version of the code that is verified to be equivalent to the extracted code.
Another approach was used in the Flyspeck project, which used an English text as the blueprint for the formal proof scripts. Both the blueprint and proof scripts were written by humans, and the alignment between them was also a human effort. I wish to avoid that labor-heavy style in the formal abstracts project.
Also, in the proof of the Kepler conjecture, the C++ code to rigorously test nonlinear inequalities by interval arithmetic was automatically generated from the formal specification of the inequalities in HOL Light.
The foundational back ends of CNLs are too weak
The Forthel language compiles down to first order logic. The reasoning in the earlier CNL example from Rudin is not based on axiomatic reasoning using the axioms of Zermelo-Fraenkel set theory. Rather, the authors made up their own system of axioms that were designed to prove exactly what they wanted to prove. For this reason, the example is really just a toy example that is foundationally ungrounded. (Yet it is a working technology that makes us see what is concretely realizable.)
None of the successful proof assistants are based on first order logic. Most of the widely used proof assistants are based on some form of type theory (simple type theory or the calculus of inductive constructions). Proof assistants based on set theory (such as Mizar) add a layer of soft typing on top of the set theory.
I agree with this criticism. I believe that a more powerful back end is needed for a CNL if it is to be widely adopted. I propose the Lean theorem prover as a back end. This will require some changes to the grammar of the CNL.
We already have too many proof assistants and incompatible research directions.
Another CNL will further fragment research on formalization.
Interoperability is important. It emerged as a notable theme at the BigProofs2 conference. I would hope that we can achieve some interoperability with other projects such as Flexiformal math and OMDoc, Logipedia and Dedukti, and the Lean theorem prover math libraries.
A long term project might be to design a CNL that is sufficiently universal to work with different proof assistants on the back end.
In fact, there is too little activity in the CNL space right now. I hope that we can be compatible with Arnold Neumaier’s group and Peter Koepke’s.
examples
The examples in this section are hypothetical. They are based on CNL grammar rules that have not been programming into a computer. They illustrate what we hope soon to obtain. The changes to the existing production rules of Forthel are relatively minor.
To continue reading, open the pdf.
I thank Arnold Neumaier and Peter Koepke for many discussions and for getting me interested in this topic.